 La cosiddetta scuola pitagorica famosa e riservata, mostrava tutti i caratteri di chiusura quasi religiosa raccolta attorno alla figura del maestro. Il vincolo di segretezza era in realtà un legame molto forte tra gli appartenenti alla scuola e Pitagora che non lasciò nulla di scritto come i suoi discepoli; questi ultimi, di fatto, attribuivano i risultati raggiunti al grande sapiente sia per onorarlo che per rendere credibili i risultati stessi. Né possiamo pensare che, sempre seguendo la tradizione, una volta tornato a casa, convocasse attorno a un tavolo la moglie Teano, i figli Arimnesto, Telauge e Damo (femmina) per svelare la dimostrazione del suo teorema sul triangolo rettangolo. Alla radice del pensiero di Pitagora non vengono stabiliti gli elementi naturali come aria, acqua, fuoco, ma il numero naturale regola di ogni cosa, dal rapporto tra le cose al movimento dei corpi celesti, dalle forme delle figure geometriche perfette alle armonie musicali delle corde di un’arpa. Tutto si può descrivere attraverso i numeri naturali (1,2,3,…) e i loro rapporti; gli oggetti materiali o creati dalla mente, tutte le figure geometriche sono il risultato di aggregati di “monadi”, granelli unitari dotati di dimensione ma non ulteriormente divisibili, non disposti casualmente, ma secondo un ordine a fondamento dell’aritmogeometria. Il numero di monadi che compongono ogni ente è finito. Da ciò proviene la rappresentazione geometrica dei numeri poligonali (triangolari, quadrati, pentagonali,) e poliedrici (tetraedrici, piramidali quadrangolari, …)
La cosiddetta scuola pitagorica famosa e riservata, mostrava tutti i caratteri di chiusura quasi religiosa raccolta attorno alla figura del maestro. Il vincolo di segretezza era in realtà un legame molto forte tra gli appartenenti alla scuola e Pitagora che non lasciò nulla di scritto come i suoi discepoli; questi ultimi, di fatto, attribuivano i risultati raggiunti al grande sapiente sia per onorarlo che per rendere credibili i risultati stessi. Né possiamo pensare che, sempre seguendo la tradizione, una volta tornato a casa, convocasse attorno a un tavolo la moglie Teano, i figli Arimnesto, Telauge e Damo (femmina) per svelare la dimostrazione del suo teorema sul triangolo rettangolo. Alla radice del pensiero di Pitagora non vengono stabiliti gli elementi naturali come aria, acqua, fuoco, ma il numero naturale regola di ogni cosa, dal rapporto tra le cose al movimento dei corpi celesti, dalle forme delle figure geometriche perfette alle armonie musicali delle corde di un’arpa. Tutto si può descrivere attraverso i numeri naturali (1,2,3,…) e i loro rapporti; gli oggetti materiali o creati dalla mente, tutte le figure geometriche sono il risultato di aggregati di “monadi”, granelli unitari dotati di dimensione ma non ulteriormente divisibili, non disposti casualmente, ma secondo un ordine a fondamento dell’aritmogeometria. Il numero di monadi che compongono ogni ente è finito. Da ciò proviene la rappresentazione geometrica dei numeri poligonali (triangolari, quadrati, pentagonali,) e poliedrici (tetraedrici, piramidali quadrangolari, …)
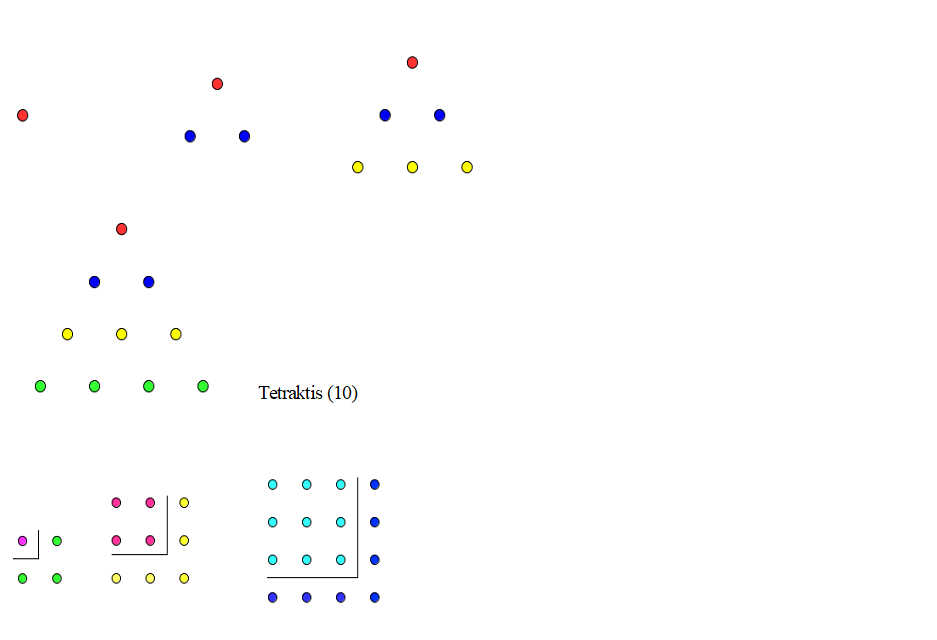
Quadrati
(https://areeweb.polito.it/didattica/polymath/htmlS/argoment/ParoleMate/Mag_09/Aritmogeometria.htm
 Si può notare come se si addiziona al primo dispari 1 il successivo dispari 3 (palline verdi), si ottiene un quadrato 4; se si addiziona a 4 il successivo dispari 5 (palline gialle), si ottiene un quadrato 9; se si addiziona a 9 il successivo numero dispari (di 5) 7(paline blu), si ottiene il successivo quadrato 16. E così di seguito.
Si può notare come se si addiziona al primo dispari 1 il successivo dispari 3 (palline verdi), si ottiene un quadrato 4; se si addiziona a 4 il successivo dispari 5 (palline gialle), si ottiene un quadrato 9; se si addiziona a 9 il successivo numero dispari (di 5) 7(paline blu), si ottiene il successivo quadrato 16. E così di seguito.
I pitagorici conoscevano i numeri perfetti (numeri uguali alla somma dei loro divisori (Es: 6= 3+2+1); i numeri gemelli: coppie di numeri primi distanti solo di un posto nella serie dei numeri naturali (Es: 5-7; 17-19) e così via; i numeri amici: coppie di numeri tali che ognuno di essi è la somma dei divisori dell’altro (Es: 220-284, 2620-2924). Grazie a potenti pc al momento si conoscono12 milioni di coppie di numeri amici, ma non si può ancora dire se sono infiniti o no. Le convinzioni numeriche dei pitagorici sono ancor più avvalorate dai legami aritmetici tra i diversi suoni emessi da una corda tesa pizzicata in punti diversi. La tradizione vuole che sia stato proprio Pitagora a scoprire tale legame quando si trovò a passare davanti alla bottega di un fabbro e si mise ad ascoltare i suoni provenienti dal battere dei martelli sull’incudine. Studiando le corde sottoposte a pizzicate, Pitagora comprese la relazione esistente tra la lunghezza della corda (dove viene pizzicata) e le relazioni armoniche descritte dai rapporti fra numeri naturali. Esiste però un’altra leggenda più antica che riguarda due fratelli: Tubalkain (il primo fabbro della storia) e Iubal (il primo musico inventore della cetra). Sono figli di Lamech e madri distinte; Lamech è discendente diretto di Caino. La rappresentazione è la stessa: Tubalkain batte col martello e Iubal ascolta e crea una teoria musicale. È probabile che le prime turbolenze numeriche Pitagora le abbia trovate proprio nei rapporti numerici per le pizzicate alle corde in modo da ottenere i risultati armonici sperati piuttosto che nel triangolo rettangolo. Si può ragionevolmente presumere che Pitagora o i pitagorici siano giunti alla dimostrazione del teorema di Pitagora che si può enunciare nella forma seguente: “Nel triangolo rettangolo l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei due quadrati costruiti sui cateti”. Vale anche l’inverso: se in un triangolo l’area del quadrato costruito su un lato è uguale alla somma delle aree dei quadrati costruiti sugli altri due lati, allora il triangolo è rettangolo. Al posto della parola quadrato si può sostituire la parola “triangolo equilatero” oppure qualsiasi poligono regolare (pentagono, esagono…) e il teorema continua a valere (anche se non l’abbiamo imparato a scuola) ugualmente per “semicerchio”: in un triangolo rettangolo il semicerchio che ha come diametro l’ipotenusa è equiesteso alla somma dei semicerchi che hanno come diametri i cateti. Molti si sono cimentati nel cercare una dimostrazione del teorema come Leonardo da Vinci o James Abram Garfield (1931-1881) ventesimo presidente degli Stati Uniti. Esistono moltissime diverse dimostrazioni del teorema di Pitagora e più di 360 sono raccolte nel testo di Elisa Scott Loomis: The Pythagorean Proposition (1968). Difficile stabilire la data della comparsa del teorema per la prima volta, ma si è certi che questo avvenne un migliaio di anni prima di Pitagora. La relazione del tipo a2 + b2 = c2 nota come terna pitagorica, era conosciuta in Mesopotamia dalla prima metà del secondo millennio a. C. e veniva insegnata nelle scuole degli scribi. Testimonianze egizie risalenti al 1400 a.C. si trovano su alcune tombe a Tebe (dove Porfirio colloca Pitagora nel suo soggiorno egizio) e per la precisione si legge la terna 32 +42 = 52. Nel 1945 venne scoperta una tavoletta 
Riferimenti
Diogene Laerzio, Vite dei filosofi, TEA, 1993.
Maria Timpanaro Cardini (a cura di), Pitagorici Antichi. Testimonianze e frammenti, Bompiani, 2010.
Kitty Ferguson, La musica di Pitagora, Longanesi 2009.
Bruno D'Amore, Silvia Sbaragli, La Matematica e la sua storia, volume1, Dedalo, 2017.
La prima immagine di Pitagorra risulta di pubblico dominio: La seconda riproduce un'opera di Luca della Robbia (1400-1482) ed è Creative Commons (CC By 3,0)
Per leggere le precedenti puntate cliccare qui sotto:
PRIMA PUNTATA
